ASYMPTOTY FUNKCJI
ASYMPTOTA PIONOWA
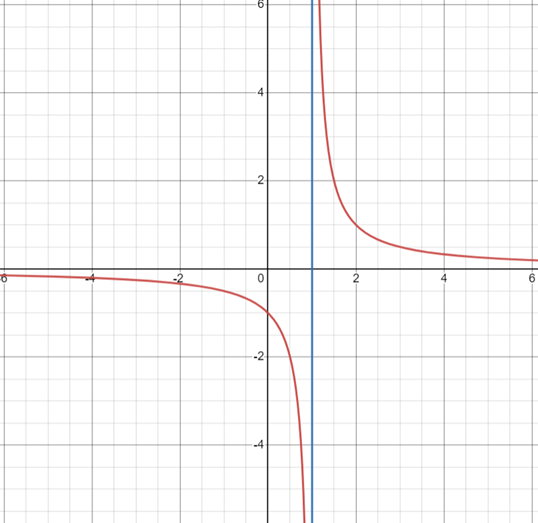
Asymptoty pionowe znajdujemy obliczając granice w punktach, które zostały odrzucone z dziedziny funkcji. Przykładowo funkcja:
\[ f(x) = \frac{x^2 – 5}{x – 2} \]
Funkcja ma dziedzinę: \( D = \mathbb{R} \backslash \{2\} \).
Aby znaleźć asymptotę pionową, obliczamy granice:
\[ \lim_{{x \to 2^-}} f(x) \quad \text{oraz} \quad \lim_{{x \to 2^+}} f(x) \]
W co najmniej jednej z tych granic powinien wyniknąć wynik \(\pm \infty\). Jeśli w obu granicach otrzymujemy liczby, np. \(3\) i \(3\),wtedy asymptota pionowa nie istnieje.
ASYMPTOTA POZIOMA
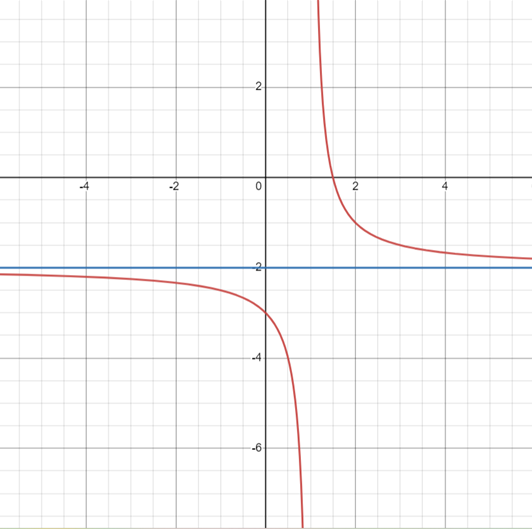
Asymptotę poziomą znajdujemy obliczając granice według wzorów:
\[
\lim_{{x \to \pm \infty}} \frac{f(x)}{x} \quad \text{oraz} \quad \lim_{{x \to \pm \infty}} f(x)
\]
Aby znaleźć asymptotę poziomą, granice:
\[
\lim_{{x \to \pm \infty}} \frac{f(x)}{x}
\]
muszą się równać \(0\).
ASYMPTOTA UKOŚNA
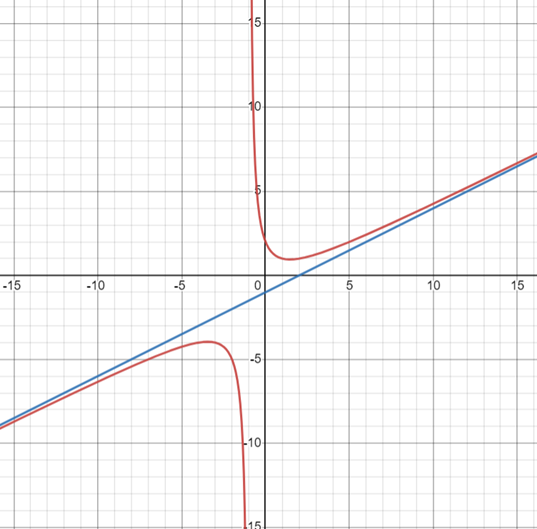
Asymptotę ukośną znajdujemy obliczając granice według wzorów:
\[
\lim_{{x \to \pm \infty}} \frac{f(x)}{x} = A \quad \text{oraz} \quad \lim_{{x \to \pm \infty}} \left[f(x) – Ax\right] = B
\]
Obliczając granice z wymienionych wzorów, możemy wyznaczyć \(A\) oraz \(B\), dzięki którym wyznaczymy asymptotę ukośną \(y = Ax + B\).