punkt przegięcia, wypukłość i wklęsłość funkcji
PUNKT PRZEGIĘCIA
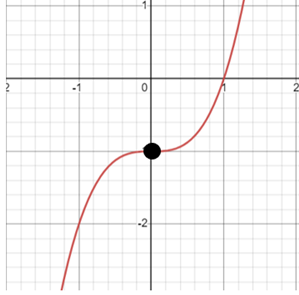
Punkt przegięcia to miejsce, w którym krzywa przestaje się wyginać w jednym kierunku i zaczyna wyginać się w drugim. Czyli punkt gdzie funkcja zmienia się z wklęsłej na wypukłą lub odwrotnie.
Jak obliczyć?:
- Obliczasz I i II pochodną funkcji
- Przyrównujesz do 0
- Sprawdzasz czy wynik należy do dziedziny
- sprawdzasz znaki po jednej i drugiej stronie funkcji
- jak z dwóch stron są różne znaki, mamy punkt przegięcia.
FUNKCJA WYPUKŁA
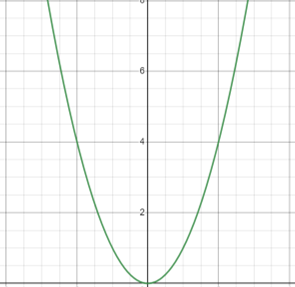
Jak obliczyć?:
- Obliczasz I i II pochodną funkcji
- Przyrównujesz do nierówności >
- Rozwiązujesz nierówność
FUNKCJA WKLĘSŁA
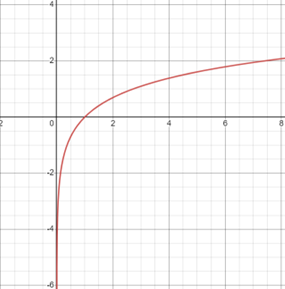
Jak obliczyć?:
- Obliczasz I i II pochodną funkcji
- Przyrównujesz do nierówności < 0
- Rozwiązujesz nierówność
1. Wyznacz punkty przegięcia oraz przedziały wklęsłości i wypukłości funkcji: $$f\left(x\right)=x^3-9x^2+1$$
2. Wyznacz punkty przegięcia oraz przedziały wklęsłości i wypukłości funkcji: $$f\left(x\right)=x^4-x^5$$
3. Wyznacz punkty przegięcia oraz przedziały wklęsłości i wypukłości funkcji: $$f\left(x\right)=x+\frac1x$$
4. Wyznacz punkty przegięcia oraz przedziały wklęsłości i wypukłości funkcji: $$f\left(x\right)=\frac{3x^2}{1-x}$$
5. Wyznacz punkty przegięcia oraz przedziały wklęsłości i wypukłości funkcji: $$f\left(x\right)=\frac x{1-x^2}$$
rozwiązanie
\[ f\left(x\right)=\frac1{x^3}+\frac1{x^2}\]
Dziedzina funkcji: \( D=\mathbb{R}\backslash\left\{0\right\}\)
Pierwsza pochodna funkcji:
$$f’\left(x\right)=-\frac{3+2x}{x^4}$$
Druga pochodna funkcji:
$$f”\left(x\right)=\frac{12+6x}{x^5}$$
Wyznaczmy punkty przegięcia:
$$f”\left(x\right)=0\\\frac{12+6x}{x^5}=0\\12+6x=0\\x=-2$$
czyli punkt x=-2 jest podejrzany o bycie punktem przegięcia. Sprawdzamy znaki po lewej i prawej stronie funkcji.
Zacznijmy od lewej strony. Bierzesz dowolny punkt na lewo od -2, np. -3.
Podstawiamy ten punkt pod funkcję na drugą pochodną:$$f”\left(-3\right)=\frac{12+6\cdot\left(-3\right)}{\left(-3\right)^5}=\frac2{81}$$
Wynik jest dodatni
Teraz dowolny punkt na prawo w przedziale (-2, 0) np. -1. Podstawiamy ten punkt pod funkcję na drugą pochodną: $$f”\left(-1\right)=\frac{12+6\cdot\left(-1\right)}{\left(-1\right)^5}=-6$$
Wynik jest ujemny
Otrzymaliśmy z obydwu stron różne znaki, czyli x=-2 jest naszym punktem przegięcia.
Wartość dla tego punktu: $$f\left(-2\right)=\frac1{\left(-2\right)^3}+\frac1{\left(-2\right)^2}=\frac18$$
Wyznaczmy przedział wklęsłości:
$$f”\left(x\right)<0\\\frac{12+6x}{x^5}<0\\x\in\left(-2,0\right)$$
Przedział wypukłości:
$$f”\left(x\right)>0\\\frac{12+6x}{x^5}>0\\x\in\left(-\infty,-2\right)\vee\left(0,+\infty\right)$$